Newton–Euler equations
The Newton–Euler equations describe the combined translational and rotational dynamics of a rigid body.[1][2] [3][4][5] With respect to a coordinate frame whose origin coincides with the body's center of mass, they can be expressed in matrix form as:
where
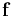 = total force acting on the center of mass
= total force acting on the center of mass = mass of the body
= mass of the body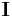 = the identity matrix
= the identity matrix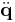 = acceleration of the center of mass
= acceleration of the center of mass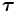 = total torque (or moment) acting about the center of mass
= total torque (or moment) acting about the center of mass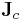 = moment of inertia about the center of mass
= moment of inertia about the center of mass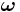 = angular velocity of the body
= angular velocity of the body
With respect to a coordinate frame that is not coincident with the center of mass, the equations assume the more complex form:
where 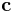 is the location of the center of mass, and
is the location of the center of mass, and
denotes a skew-symmetric cross product matrix.
The inertial terms are contained in the spatial inertia matrix
while the fictitious forces are contained in the term
When the center of mass is not coincident with the coordinate frame (that is, when 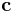 is nonzero), the translational and angular accelerations (
is nonzero), the translational and angular accelerations (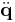 and
and 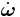 ) are coupled, so that each is associated with force and torque components.
) are coupled, so that each is associated with force and torque components.
The Newton–Euler equations are used as the basis for more complicated "multi-body" formulations that describe the dynamics of systems of rigid bodies connected by joints and other constraints. Multi-body problems can be solved by a variety of numerical algorithms.[6][2][7]
References
- ^ Hubert Hahn (2002). Rigid Body Dynamics of Mechanisms. Springer. p. 143. ISBN 3540423737. http://books.google.com/books?id=MqrN3KY7o6MC&pg=PA143&dq=EUler+equations+%22rigid+body%22&lr=&as_brr=0&sig=ACfU3U00jfE08smw1IqJt69QdcMSKvDIeA.
- ^ a b Ahmed A. Shabana (2001). Computational Dynamics. Wiley-Interscience. p. 379. ISBN 9780471371441. http://books.google.com/books?id=dGfcbOsm2PwC&pg=PA379&dq=EUler+equations+%22rigid+body%22&lr=&as_brr=0&sig=ACfU3U01BZBb84es37aiHVpdE33IdGze-A.
- ^ Haruhiko Asada, Jean-Jacques E. Slotine (1986). Robot Analysis and Control. Wiley/IEEE. pp. §5.1.1, p. 94. ISBN 0471830291. http://books.google.com/books?id=KUG1VGkL3loC&pg=PA94&dq=EUler+equations+%22rigid+body%22&lr=&as_brr=0&sig=ACfU3U3LiZyQRj0zYXQ8ON2zwuiiwQO7dA.
- ^ Robert H. Bishop (2007). Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling. CRC Press. pp. §7.4.1, §7.4.2. ISBN 0849392586. http://books.google.com/books?id=3UGQsi6VamwC&pg=PT104&dq=EUler+equations+%22rigid+body%22&lr=&as_brr=0&sig=ACfU3U1DtQ2BGV_Q34yAj-WhnQ4tStxPCw#PPT104,M1.
- ^ Miguel A. Otaduy, Ming C. Lin (2006). High Fidelity Haptic Rendering. Morgan and Claypool Publishers. p. 24. ISBN 1598291149. http://books.google.com/books?id=lk0StvDRoEMC&pg=PA24&dq=EUler+equations+%22rigid+body%22&lr=&as_brr=0&sig=ACfU3U0iOPnq-nMrS34O40ZMt0EbJEqu6g#PPA24,M1.
- ^ a b Roy Featherstone (2008). Rigid Body Dynamics Algorithms. Springer. ISBN 978-0-387-74314-1. http://books.google.ca/books?id=UjWbvqWaf6gC&printsec=frontcover&dq=Rigid+Body+Dynamics+Algorithms.
- ^ Constantinos A. Balafoutis, Rajnikant V. Patel (1991). Dynamic Analysis of Robot Manipulators: A Cartesian Tensor Approach. Springer. Chapter 5. ISBN 0792391454. http://books.google.com/books?id=7BcpyUjmLpUC&pg=PT195&dq=%22Kane%27s+dynamical+equations%22&lr=&as_brr=0&sig=ACfU3U1m290WlCUy1101Oj9Z9w3j5a4Lww#PPT151,M1.
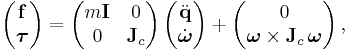
![\left(\begin{matrix} {\bold f} \\ {\boldsymbol \tau} \end{matrix}\right) =
\left(\begin{matrix} m {\bold I} & - m [{\bold c}]\\
m [{\bold c}] & {\bold J}_c - m [{\bold c}][{\bold c}]\end{matrix}\right)
\left(\begin{matrix} \ddot {\bold q} \\ \dot {\boldsymbol \omega} \end{matrix}\right) %2B
\left(\begin{matrix} {m \boldsymbol \omega} \times \left({\boldsymbol \omega} \times {\bold c}\right) \\
{\boldsymbol \omega} \times ({\bold J}_c - m [{\bold c}][{\bold c}])\, {\boldsymbol \omega} \end{matrix}\right),](/2012-wikipedia_en_all_nopic_01_2012/I/a43529ac09ecf816228ff8d2144e73fb.png)
![[\mathbf{c}] \equiv
\left(\begin{matrix} 0 & -c_z & c_y \\ c_z & 0 & -c_x \\ -c_y & c_x & 0 \end{matrix}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/babe3c82e49d205e190a35aa54f322ad.png)
![\left(\begin{matrix} m {\bold I} & - m [{\bold c}]\\
m [{\bold c}] & {\bold J}_c - m [{\bold c}][{\bold c}]\end{matrix}\right),](/2012-wikipedia_en_all_nopic_01_2012/I/c1ff5080c09e6aa0ccad3c755ac78534.png)
![\left(\begin{matrix} {m \boldsymbol \omega} \times \left({\boldsymbol \omega} \times {\bold c}\right) \\
{\boldsymbol \omega} \times ({\bold J}_c - m [{\bold c}][{\bold c}])\, {\boldsymbol \omega} \end{matrix}\right) .](/2012-wikipedia_en_all_nopic_01_2012/I/ca6add0e5ccb392d7f4ad7d429eb4c82.png)